Выбор читателей
Популярные статьи
перпендикулярности двух прямых.
1. Если прямые L 1 и L 2 заданы общими уравнениями
А 1 х + В 1 у + С 1 = 0 и А 2 х + В 2 у + С 2 = 0,
то угол между ними равен углу между их нормалями, то есть между векторами {A 1 ,B 1 } и {A 2 ,B 2 }. Следовательно,
Условия параллельности и перпендикулярности прямых тоже сводятся к условиям параллельности и перпендикулярности нормалей:
Условие параллельности, (7.11)
![]() - условие перпендикулярности. (7.12).
- условие перпендикулярности. (7.12).
2. Если прямые заданы каноническими уравнениями (7.5), по аналогии с пунктом 1 получим:
 , (7.13)
, (7.13)
Условие параллельности, (7.14)
![]() - условие перпендикулярности. (7.16).
- условие перпендикулярности. (7.16).
Здесь и - направляющие векторы прямых.
3. Пусть прямые L 1 и L 2 заданы уравнениями с угловыми коэффициентами (7.8)
у = k 1 x +b 1 и y = k 2 x + b 2 , где ![]() , а α 1 и α 2 – углы наклона прямых к оси Ох, то для угла φ между прямыми справедливо равенство: φ = α 2 - α 1 . Тогда
, а α 1 и α 2 – углы наклона прямых к оси Ох, то для угла φ между прямыми справедливо равенство: φ = α 2 - α 1 . Тогда
Условие параллельности имеет вид: k 1 =k 2 , (7.18)
условие перпендикулярности – k 2 =-1/k 1 , (7.19)
поскольку при этом tgφ не существует.
Расстояние от точки до прямой.
Рассмотрим прямую L и проведем перпендикуляр ОР к ней из начала координат (предполагаем, что прямая не проходит через начало координат). Пусть n – единичный вектор, направление которого совпадает с ОР. Составим уравнение прямой L, в которое входят два параметра: р – длина отрезка ОР и α – угол между ОР и Ох.
Для точки М, лежащей на L, проекция вектора ОМ на прямую
ОР равна р. С другой стороны, пр n OM=n·OM. Поскольку
n ={cosα , sinα }, a OM ={x,y }, получаем, что
x cosα + y sinα = p, или
x cosα + y sinα - p = 0 - (7.20)
Искомое уравнение прямой L , называемое нормальным
уравнением прямой (термин «нормальное уравнение» связан
с тем, что отрезок ОР является перпендикуляром, или нормалью, к данной прямой).
Определение 7.2. Если d – расстояние от точки А до прямой L , то отклонение δ точки А от прямой L есть число +d , если точка А и начало координат лежат по разные стороны от прямой L , и число –d , если они лежат по одну сторону от L .
Теорема 7.1. Отклонение точки А(х 0 ,у 0 ) от прямой L , заданной уравнением (7.20), определяется по формуле:
Доказательство.
Проекция OQ вектора ОА на направление ОР равна
n·OA =x 0 cosα + y 0 sinα. Отсюда δ = PQ=OQ-OP=OQ-p =
x 0 cosα + y 0 sinα - p , что и требовалось доказать
Следствие.
Расстояние от точки до прямой определяется так:
Замечание. Для того, чтобы привести общее уравнение прямой к нормальному виду, нужно умножить его на число , причем знак выбирается противоположным знаку свободного члена С в общем уравнении прямой. Это число называется нормирующим множителем.
Пример. Найдем расстояние от точки А (7,-3) до прямой, заданной уравнением
3х + 4у + 15 = 0. А ² + B ²=9+16=25, C =15>0, поэтому нормирующий множитель равен
1/5, и нормальное уравнение прямой имеет вид: ![]() Подставив в его левую часть вместо х и у координаты точки А,
получим, что ее отклонение от прямой равно
Подставив в его левую часть вместо х и у координаты точки А,
получим, что ее отклонение от прямой равно
![]() Следовательно, расстояние от точки А
до данной прямой равно 4,8.
Следовательно, расстояние от точки А
до данной прямой равно 4,8.
8. Прямая и плоскость в пространстве. Уравнения плоскости и прямой в пространстве. Угол между плоскостями. Угол между прямой и плоскостью.
Отметим, что многие утверждения и формулы, касающиеся плоскости в пространстве, доказываются и выводятся так же, как при изучении прямой на плоскости, поэтому в этих случаях будут даваться ссылки на предыдущую лекцию.
Плоскость в пространстве.
Получим сначала уравнение плоскости, проходящей через точку М 0 (х 0 ,у 0 ,z 0 ) перпендикулярно вектору n = {A,B,C },называемому нормалью к плоскости. Для любой точки плоскости М(х, у, z ) вектор М 0 М = {x - x 0 , y - y 0 , z - z 0 ) ортогонален вектору n , следовательно, их скалярное произведение равно нулю:
A(x - x 0 ) + B(y - y 0 ) + C(z - z 0 ) = 0. (8.1)
Получено уравнение, которому удовлетворяет любая точка заданной плоскости – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
После приведения подобных можно записать уравнение (8.1) в виде.
Каждому школьнику, который готовится к ЕГЭ по математике, будет полезно повторить тему «Нахождение угла между прямыми». Как показывает статистика, при сдаче аттестационного испытания задачи по данному разделу стереометрии вызывают трудности у большого количества учащихся. При этом задания, требующие найти угол между прямыми, встречаются в ЕГЭ как базового, так и профильного уровня. Это значит, что уметь их решать должны все.
В пространстве существует 4 типа взаимного расположения прямых. Они могут совпадать, пересекаться, быть параллельными или скрещивающимися. Угол между ними может быть острым или прямым.
Для нахождения угла между прямыми в ЕГЭ или, например, в решении , школьники Москвы и других городов могут использовать несколько способов решения задач по данному разделу стереометрии. Выполнить задание можно путем классических построений. Для этого стоит выучить основные аксиомы и теоремы стереометрии. Школьнику нужно уметь логически выстраивать рассуждение и создавать чертежи, для того чтобы привести задание к планиметрической задаче.
Также можно использовать векторно-координатный метод, применяя простые формулы, правила и алгоритмы. Главное в этом случае - правильно выполнить все вычисления. Отточить свои навыки решения задач по стереометрии и другим разделам школьного курса вам поможет образовательный проект «Школково».
В этой статье сначала дадим определение угла между скрещивающимися прямыми и приведем графическую иллюстрацию. Далее ответим на вопрос: «Как найти угол между скрещивающимися прямыми, если известны координаты направляющих векторов этих прямых в прямоугольной системе координат»? В заключении попрактикуемся в нахождении угла между скрещивающимися прямыми при решении примеров и задач.
Навигация по странице.
К определению угла между скрещивающимися прямыми будем подходить постепенно.
Сначала напомним определение скрещивающихся прямых: две прямые в трехмерном пространстве называются скрещивающимися , если они не лежат в одной плоскости. Из этого определения следует, что скрещивающиеся прямые не пересекаются, не параллельны, и, тем более, не совпадают, иначе они обе лежали бы в некоторой плоскости.
Приведем еще вспомогательные рассуждения.
Пусть в трехмерном пространстве заданы две скрещивающиеся прямые a и b . Построим прямые a 1 и b 1 так, чтобы они были параллельны скрещивающимся прямым a и b соответственно и проходили через некоторую точку пространства M 1 . Таким образом, мы получим две пересекающиеся прямые a 1 и b 1 . Пусть угол между пересекающимися прямыми a 1 и b 1 равен углу . Теперь построим прямые a 2 и b 2 , параллельные скрещивающимся прямым a и b соответственно, проходящие через точку М 2 , отличную от точки М 1 . Угол между пересекающимися прямыми a 2 и b 2 также будет равен углу . Это утверждение справедливо, так как прямые a 1 и b 1 совпадут с прямыми a 2 и b 2 соответственно, если выполнить параллельный перенос, при котором точка М 1 перейдет в точку М 2 . Таким образом, мера угла между двумя пересекающимися в точке М прямыми, соответственно параллельными заданным скрещивающимся прямым, не зависит от выбора точки М .
Теперь мы готовы к тому, чтобы дать определение угла между скрещивающимися прямыми.
Определение.
Угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым.
Из определения следует, что угол между скрещивающимися прямыми также не будет зависеть от выбора точки M . Поэтому в качестве точки М можно взять любую точку, принадлежащую одной из скрещивающихся прямых.
Приведем иллюстрацию определения угла между скрещивающимися прямыми.

Так как угол между скрещивающимися прямыми определяется через угол между пересекающимися прямым, то нахождение угла между скрещивающимися прямыми сводится к нахождению угла между соответствующими пересекающимися прямыми в трехмерном пространстве.
Несомненно, для нахождения угла между скрещивающимися прямыми подходят методы, изучаемые на уроках геометрии в средней школе. То есть, выполнив необходимые построения, можно связать искомый угол с каким-либо известным из условия углом, основываясь на равенстве или подобии фигур, в некоторых случаях поможет теорема косинусов , а иногда к результату приводит определение синуса, косинуса и тангенса угла прямоугольного треугольника.
Однако очень удобно решать задачу нахождения угла между скрещивающимися прямыми методом координат. Именно его и рассмотрим.
Пусть в трехмерном пространстве введена Oxyz (правда, во многих задачах ее приходится вводить самостоятельно).
Поставим перед собой задачу: найти угол между скрещивающимися прямыми a и b , которым соответствуют в прямоугольной системе координат Oxyz некоторые уравнения прямой в пространстве .
Решим ее.
Возьмем произвольную точку трехмерного пространства М и будем считать, что через нее проходят прямые a 1 и b 1 , параллельные скрещивающимся прямым a и b соответственно. Тогда искомый угол между скрещивающимися прямыми a и b равен углу между пересекающимися прямыми a 1 и b 1 по определению.
Таким образом, нам осталось найти угол между пересекающимися прямыми a 1 и b 1 . Чтобы применить формулу для нахождения угла между двумя пересекающимися прямыми в пространстве нам нужно знать координаты направляющих векторов прямых a 1 и b 1 .
Как же мы их можем получить? А очень просто. Определение направляющего вектора прямой позволяет утверждать, что множества направляющих векторов параллельных прямых совпадают. Следовательно, в качестве направляющих векторов прямых a 1
и b 1
можно принять направляющие векторы ![]() и
и ![]() прямых a
и b
соответственно.
прямых a
и b
соответственно.
Итак, угол между двумя скрещивающимися прямыми a
и b
вычисляется по формуле
 , где
, где ![]() и
и ![]() - направляющие векторы прямых a
и b
соответственно.
- направляющие векторы прямых a
и b
соответственно.
Формула для нахождения косинуса угла между скрещивающимися прямыми
a
и b
имеет вид  .
.
Позволяет найти синус угла между скрещивающимися прямыми, если известен косинус: ![]() .
.
Осталось разобрать решения примеров.
Пример.
Найдите угол между скрещивающимися прямыми a
и b
, которые определены в прямоугольной системе координат Oxyz
уравнениями ![]() и
и  .
.
Решение.
Канонические уравнения прямой в пространстве позволяют сразу определить координаты направляющего вектор этой прямой – их дают числа в знаменателях дробей, то есть, ![]()
![]() . Параметрические уравнения прямой в пространстве также дают возможность сразу записать координаты направляющего вектора – они равны коэффициентам перед параметром, то есть,
. Параметрические уравнения прямой в пространстве также дают возможность сразу записать координаты направляющего вектора – они равны коэффициентам перед параметром, то есть, ![]() - направляющий вектор прямой
- направляющий вектор прямой  . Таким образом, мы располагаем всеми необходимыми данными для применения формулы, по которой вычисляется угол между скрещивающимися прямыми:
. Таким образом, мы располагаем всеми необходимыми данными для применения формулы, по которой вычисляется угол между скрещивающимися прямыми:
Ответ:
Угол между заданными скрещивающимися прямыми равен .
Пример.
Найдите синус и косинус угла между скрещивающимися прямыми, на которых лежат ребра AD и BC пирамиды АВСD , если известны координаты ее вершин: .
Решение.
Направляющими векторами скрещивающихся прямых AD
и BC
являются векторы и . Вычислим их координаты как разность соответствующих координат точек конца и начала вектора:
По формуле  мы можем вычислить косинус угла между указанными скрещивающимися прямыми:
мы можем вычислить косинус угла между указанными скрещивающимися прямыми:
Теперь вычислим синус угла между скрещивающимися прямыми:
Параллельные прямые
. Расстояние между
параллельными прямыми
.
.
Соответственные углы
.
Внутренние и внешние накрест
лежащие углы
.
Внутренние и внешние односторонние углы .
Углы с соответственно
перпендикулярными сторонами
.
Пропорциональные отрезки
.
Теорема Фалеса.
Две прямые AB и CD ( рис.11 ) называются параллельными , если они лежат в одной плоскости и не пересекаются, сколько бы их ни продолжать. Обозначение: AB || CD . Все точки одной параллельной прямой находятся на одинаковом расстоянии от другой параллельной прямой. Все прямые, параллельные одной прямой, параллельны между собой. Принято считать, что угол между параллельными прямыми равен нулю. Угол между двумя параллельными лучами равен нулю, если у них одинаковые направления, и 180 ° , если их направления противоположны. Все перпендикуляры ( AB , CD , EF , рис.12) к одной и той же прямой KM параллельны между собой. Обратно, прямая KM , перпендикулярная к одной из параллельных прямых, перпендикулярна и к остальным. Длина отрезка перпендикуляра, заключённого между двумя параллельными прямыми, есть расстояние между ними.
При пересечении двух параллельных прямых третьей прямой, образуются восемь углов (рис.13), которые попарно называются:
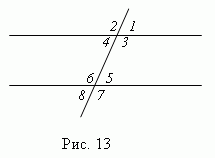
1) соответственные углы (1 и 5; 2 и 6; 3 и 7; 4 и 8 ); эти углы попарно
равны: ( 1 = 5; 2 = 6; 3 = 7; 4 = 8 );
2) внутренние накрест лежащие углы (4 и 5; 3 и 6 ); они попарно равны;
3) внешние накрест лежащие углы (1 и 8; 2 и 7 ); они попарно равны;
4) внутренние односторонние углы (3 и 5; 4 и 6 ); их сумма равна 180 °
( 3 + 5 = 180
° ; 4 + 6 = 180 ° );5) внешние односторонние углы (1 и 7; 2 и 8 ); их сумма равна 180 °
( 1 + 7 = 180 ° ; 2 + 8 = 180 ° ).
Углы с соответственно параллельными сторонами либо равны друг другу ( если они оба острые, или оба тупые, 1 = 2 , рис.14), либо их сумма равна 180 ° ( 3 + 4 = 180 ° , рис.15).
| Статьи по теме: | |
|
"Духота и трупный запах": детские воспоминания о Сталинградской битве Воспоминания участников сталинградской битвы читать
В начале 70-х годов поздней осенью, когда уже выпал первый снег, мне... Трубецкой дети. Биографии декабристок. Биография Екатерины
Ивановны Трубецкой
План Введение 1 Биография 2 Жена декабриста 3 Произведения,... Анализ рассказа «Жизнь Василия Фивейского» Андреева Л
Жизнь Василия Фивейского Над всей жизнью Василия Фивейского тяготел... | |